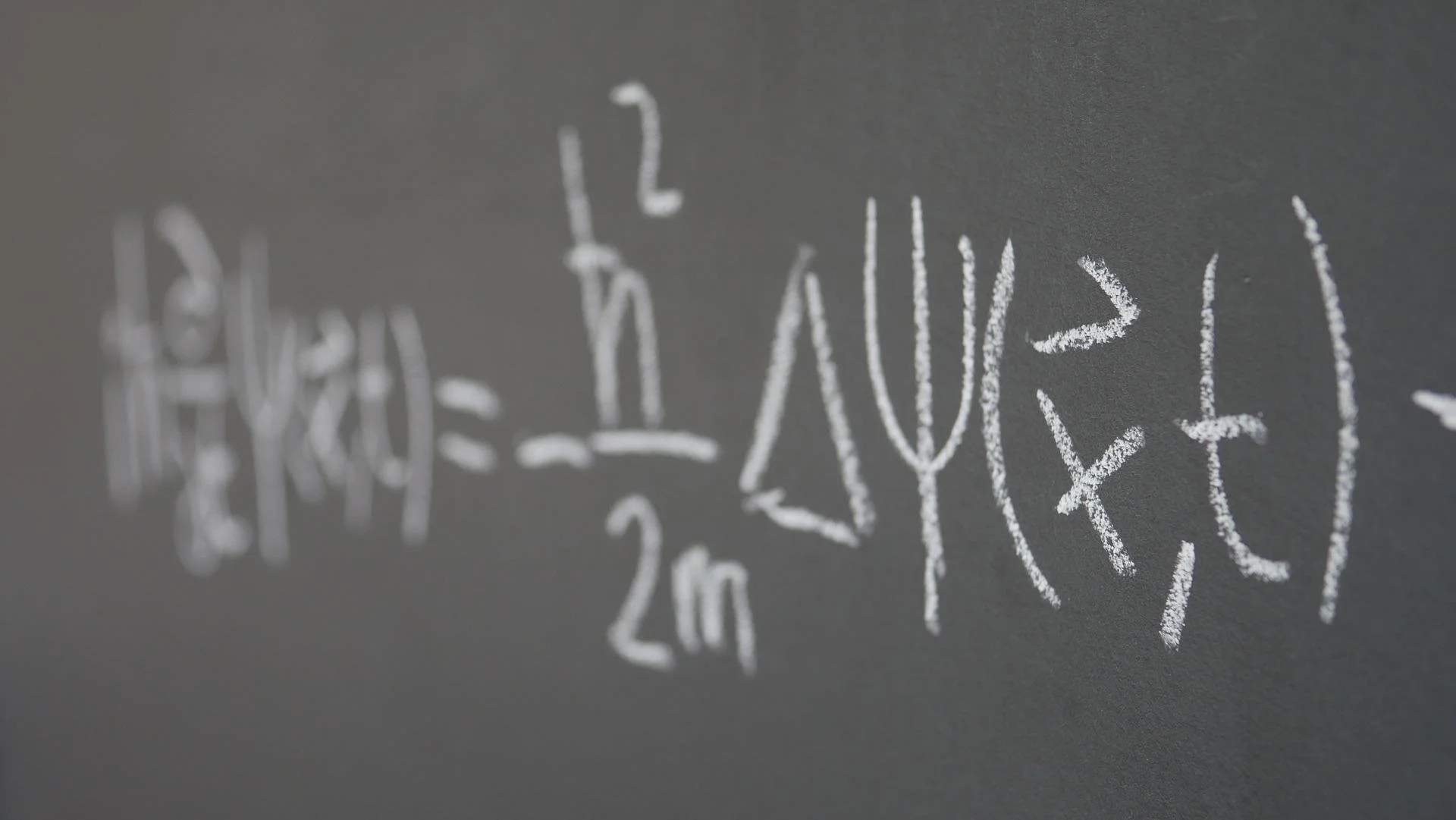Part 2! How do physicists understand quantum mechanics? What are the postulates and principles of quantum mechanics? How do the foundations of quantum mechanics compare to other theories? I discuss these questions and more in today’s Ask a Spaceman!
This episode is sponsored by BetterHelp. Give online therapy a try at betterhelp.com/spaceman and get on your way to being your best self. Visit BetterHelp to get 10% off your first month!
Support the show: http://www.patreon.com/pmsutter
All episodes: http://www.AskASpaceman.com
Follow on Twitter: http://www.twitter.com/PaulMattSutter
Like on Facebook: http://www.facebook.com/PaulMattSutter
Watch on YouTube: http://www.youtube.com/PaulMSutter
Read a book: http://www.pmsutter/book
Go on an adventure: http://www.AstroTours.co
Keep those questions about space, science, astronomy, astrophysics, physics, and cosmology coming to #AskASpaceman for COMPLETE KNOWLEDGE OF TIME AND SPACE!
Big thanks to my top Patreon supporters this month: Justin G, Chris L, Barbara K, Duncan M, Corey D, Justin Z, Andrew F, Naila, Scott M, Rob H, Justin, Louis M, John W, Alexis, Erin J, Jennifer M, Gilbert M, Joshua, Bob H, John S, Thomas D, Michael R, Simon G, David B, Frank T, Tim R, Tom Van S, Mark R, Alan B, Craig B, Richard K, Dave L, Stephen M, Maureen R, Stace J, Neil P, COTFM, Stephen S, Ken L, Alberto M, Matt C, Joe R, David P, Ulfert B, Sean M, Edward K, Darren W, Tracy F, Sarah K, Steven S, Ryan L, Ella F, Richard S, Sam R, Thomas K, James C, Jorg D, R Larche, Syamkumar M, John S, Fred S, Homer V, Mark D, Colin B, Bruce A, Steven M, Brent B, Bill E, Tim Z, Thomas W, Linda C, David W, Aissa F, Marc H, Avery P, Scott M, Thomas H, Farshad A, Matthias S, Kenneth D, Maureen R, Michael W, Scott W, David W, Neuterdude, Cha0sKami, Robert C, Matthew K, Robert B, Gary K, Stephen J, dhr18, Anna V, Johanna M, Matthew G, Paul & Giulia S, Ron D, Steven M, Louis M, Michael C, Alyssa K, Lode D, Roger, Bob C, Patti H, Red B, Benjamin M, BlueDragon, Stephen A, Ian S, James R, Skip M, Robert O, and Adam I!
Thanks to Cathy Rinella for editing. Special effects from Freesound: finalobserver (CC-0) and aldy505 (CC-by-3.0)
Hosted by Paul M. Sutter, astrophysicist and the one and only Agent to the Stars (http://www.pmsutter.com).
All Episodes | Support | iTunes | Spotify | YouTube
EPISODE TRANSCRIPTION (AUTO-GENERATED)
For the three of you tuning in. Welcome to Paul Sutter's Quantum Mechanics 102 Class. There will be a quiz on Friday, and your essays on What if I Want to Be Schrodinger's Cat are due next week. So what do we have so far? This is part two of, um, a certain length of a series that is yet to be determined in the true quantum spirit on quantum mechanics. Uh, last time we saw where quantum mechanics fits into the larger tapestry of physics, what was the turf of quantum mechanics was the domain or realm of quantum mechanics. Where does it apply and where does it not apply and why quantum mechanics is here and what we're gonna do about it? What do we have? Quantum mechanics is a set of math equations that tell us how to make predictions about the behavior of the small and slow part of the universe, namely subatomic particles doing their usual subatomic thing, but not very quickly, as in not close to the speed of light.
That's what quantum mechanics is. That's it. It's a set of math equations. Now we are going in this series to explore the history and the connection to experiments And what? This teaches us about the fundamental nature of reality, at least at the subatomic level. But we're not there yet. First, we need to understand what quantum mechanics actually is. What are these math equations? What are the predictions they make? How does a physicist understand quantum mechanics? Now, I'm not going to literally read math equations to you because that wouldn't be productive for either of us. But I am going to tell you about the postulates of quantum mechanics. Now, postulate is a very special word. It's one of the biggest word in physics. It is the ground assumptions, like like Like say, you're the first physicist ever, and you're born into the world and you see a natural phenomenon.
The sun goes down behind the horizon and it gets dark. You pour water and the water falls to the ground. You see a lightning storm and you get struck by lightning. You're surrounded by natural phenomena, and you need you're a physicist, so you want to build a mathematical description of this world so you can go out and make predictions and verify against experiment. Do all of your normal physics science Y things, but you need to start somewhere. You need to start with some hypothesis. You need to start with some basic guess, some basic statement about the world. And when you make a basic statement in mathematics or physics that is called a postulate, it is the ground assumption. Now, these postulates in quantum mechanics the ground truth statements from which the entire rest of quantum mechanics flows. Which is why I want to talk about the postulates because that is the core that is the real bare bones foundation cornerstone of quantum mechanics.
Everything else that we are gonna talk about in quantum mechanics stems and flows from those postulates. Now, I'm gonna tell you off the bat that these postulates these statements that we're going to accept as factor these these basic things we're gonna say about the world. Yes, we do accept them as fact, uh, later on, we go to test them when we go to test the actual theory. Uh, these postulates are super abstract. At first glance, they don't connect to anything in the physical world. At first glance, you'll be left wondering How is this even physics? What Are we even saying? What does this have to do with actual observations? They just seem like a bunch of bizarre random statements like you woke up in the middle of algebra two class and have no clue what page you're on. The postulates of quantum mechanics are very abstract, and this is in contrast to the postulates that ground other physical theories. So, for example, the ground assumption postulate of special relativity.
There's just one, actually, and you can decide you have some flexibility of how you say it. Say, say it where you want to start from. But one way to say it. One way to frame it in special relativity is to start with the assumption that the speed of light is constant from that statement. If you just say, I believe that the speed of light is constant from there you can work out the mathematics. You have all of special relativity length contraction, time dilation, relativity of simultaneity, E equals MC squared. All of it flows from the statement. The speed of light is constant. How does it do that? Just just does that through the power of math. That's why math is so awesome. and why we use it in physics. Because then you can make a statement and then you cast it in mathematical terms, and then you can just roll with it and you can flush it out and go boom, boom, boom, boom and come up with all these other statements that surround it. And that postulate in special relativity is is very concrete.
It's very easy, like, Wow, yeah, speed of light, constant. I get it. Special relativity has that going for general relativity is based on one more postulate one more ground truth assumption about the universe, which is that the equivalence principle holds from there. You get all of general relativity in quantum mechanics. First off, we have more than one postulate because quantum mechanics is more complicated than special relativity and more complicated than general relativity. And it's very abstract, and this abstractness and and you'll get it. I'm trying to prepare you for it, because the especially the first postulate is a real doozy. This abstractness is not a bad thing. You would think that if you're you're trying to develop a physical theory of the natural world, you will want your base assumptions. Your base statements to be grounded in the physical world, something you can observe or hold or touch or smell. But no, it's actually the other way around. We actually prefer abstractness because the more abstract we are, the more general and useful and powerful we can be that way.
We're not laser focused on one particular experiment or set up or unique situation. We want to be broad. We want to capture as much phenomena as much richness that we observe in the world with as few statements as possible with as few postulates as possible. It's like a game like what is the most amount of behavior in the universe that I can explain with as few assumptions as possible? There are, of course, other ways to construct physical theories and other approaches. But this approach has served us well for a few 100 years, So why stop now and again? Don't worry if any of anything that I'm saying doesn't make sense or any of the postulates don't make sense, at least not yet. One. Quantum Mechanics doesn't really make sense anyway to anybody. So you're not alone. If if at the end of this series or the end of any of these episodes. You're just like, what is going on? Don't worry, you're not alone. Literally. Everybody is in the same boat as you. In two and later episodes, I will connect these postulate back to experiments and history and actual observations and examples.
We we will do our best to turn the abstract into the concrete. But as we get more complex and more wild and in future episodes, we're talking about the fundamental nature of reality in some super high level, mind bending way. Remember that these statements that I'm about to make are the building blocks of the theory. These are the things we assume to be true, to get the machine going now. Once the machine is going, you have to confront experiment and observation, and that's how we test the whole thing. That's why we use mathematics in physics so that we can start from postulates. Then we can grow our physical theory and we can make a prediction. And if the prediction is wrong, then we know the postulates are wrong. Mathematics allows us to build those logical chains so that we know if we're on the right path or not. So these postulates the ground truth assumptions. The most basic things we can say about the subatomic world have been tested for over a century and are probably the most well tested postulates in all of science.
And there are seven of them or I'm presenting seven postulates. There are different ways of writing these, and sometimes you'll see them combined together so you'll see different numbers. Sometimes they're presented as four postulates sometimes, uh, there are more. But in general, there's a handful of initial of initial assumptions behind quantum mechanics, and I'm choosing seven because I'm breaking them down as much as possible. I have this joke that whenever I see or hear or encounter arguments that have more than a handful of assumptions, like say, Well, well, in order for this to be true, we're gonna assume this. This, this, this this and this any time it's more than a handful, I say Congratulations. You are officially more complex than quantum mechanics. It it's not a very funny joke, and I guess I never say it out loud. But there you go. Quantum mechanics is complex, but it rests on seven statements. Think about that as we move on in this series, the richness and variety of the entire subatomic world not just a part of it, but subatomic physics overall across the universe, our entire understanding of that subatomic world rests on a handful of statements.
How powerful is that? That you can say seven things. They're between four and seven things, depending on how you break it down or combine them or merge them in those few statements completely and utterly and totally describe the entirety of the subatomic world. Everything we're going to encounter in quantum mechanics rests on these statements. But before I tell you the postulates, let's start with how a physicist sees the world. When we look at a physical system and watch it do its cute little thing, and we were to take a snapshot of that system, we would call that snapshot a state. So, for example, I throw a ball at you. I'm gonna freeze a moment in time. That moment in time is called a state. It's a complete description of what that system is doing at that specific frozen moment. So, for example, the state of the system might be include the position of the ball, the velocity of the ball, the acceleration of the ball, the temperature of the ball, the electric charge of the ball.
Yeah, everything I need to know about that system. Uh, the air temperature, the amount of sunlight, the gravitational situation, the list of all the things in that frozen moment in time. In physics language, we call that a state a complete description of what the specific system is doing in a frozen moment in time. Now, a word from our sponsor better help. One of my favorite things about being a physicist is that the training I've received in physics is training to solve problems. It's training to look at difficult, complex, mind bending problems and find a simple solutions to to take baby steps to find approximations and problem solving itself is a great skill that I found that physics has helped me with it. And you know what else can help with that?
It's therapy, I. I regularly speak with a therapist I've known and trusted this the therapist for years. Who is this person has guided me through very difficult points in my life and and moments of of easy sailing and just it's there. Someone who is close, a confidant and who also understands people, which was not a part of my physics training. If you're thinking of giving therapy a try, I want you to try better help. It's convenient, accessible, affordable, entirely online. Seriously, give it a shot. I. I can't advocate for mental health anymore. When you want to be a better problem solver therapy can get you there. Visit better help dot com slash spaceman today to get 10% off your first month. That's better. HE LP dot com slash spaceman So we have states, quantum mechanics.
We deal with a lot of states, the state of the electron, the state of the electromagnetic field and so on. We care about states, especially in quantum mechanics. Second, we have observables observables are the things that we can measure, whether it's with eyeballs or expensive laboratory equipment or whatever. Observables are the things about the state that we measure. There may be parts of the state that we can't ever directly measure. This seems weird, but remember, in the case of quantum mechanics, we're dealing with subatomic particles. I never get to actually know what an electron looks like actually looks like, and there may be properties of the electron that I can calculate, but I can never observe. Instead, I have to care about the things that I can observe. And these are the Observables, like if in my scenario where I'm analyzing the problem of throwing a ball at you, there may be a lot of things about that ball, that baseball or it could be any ball you want.
I don't care. There may be a lot of things about that ball that describe its state all the information associated with that ball that I can observe. If I'm just looking at it, I can note its position. I can estimate its velocity, but I can't know its temperature in this case because of the limitations of my experiment. The temperature is not an observable if I get out a thermometer. One of those remote infrared thermometer thing is, yeah, I can calculate its temperature, and that makes it an observable. But until then, I don't. When it comes to subatomic particles, I'm going to especially care about the things I can observe. I can observe their position, their momentum, their energy level, their spin state. These are going to be the properties that I can measure and detect. And so naturally, my physical theory is going to concern itself with these properties, the observable ones, and less so with the unobserved ones, because I'll never know if my theory is correct, because I can't test it. So observables matter.
Lastly, there needs to be some rule for taking the current state, the current snapshot in time and moving it forward in time. This is how I'm able to make predictions as a physicist. This rule tells me how the system evolves from one state to another. These are our familiar equations of motion laws. Newton's laws are a set of formulas for taking a current state and predicting what the next state is gonna be. So if I take that frozen snapshot moment in time where I have the ball frozen in midair, I can list its state and its observables its position, its momentum, its acceleration. And then, from there, I can apply Newton's laws to tell you where the ball is gonna go in the next state in the next state in the next, I'm gonna move it forward in time, and I'll be able to make a prediction. Maxwell's equations tell us how electric charges are going to move. So if I know the state of a system the current running down a wire, uh, the charge on this metal sphere, Maxwell's equations tell me how that will behave into the future.
How that one state will evolve into another. This is the construction. This is the language for for basically all physical theory, quantum or not, from throwing a ball in the air to shooting a laser to energizing an atom. This is the basic building blocks of any physical theory. All physics share the same kind of language for the theories of physics developed before quantum mechanics, which we generally call classical physics. In the same way you would call music written before a certain time period. Classical music. This was pretty straightforward. This idea of states and observables and the rules of time evolution. This was all pretty straightforward, so straightforward that nobody really talked about it, and everyone just agreed that this was the best way to view nature through a physics lens. As we'll see with quantum mechanics, the relationship between time, evolution, observable and state get a little fuzzy. The postulates of quantum mechanics tell us, what is the state when it comes to quantum mechanics?
What are the observables and what is the evolution through time? That's what the postulates do. They they set up the problem. They take this common language of states Po, uh, observables time evolution The postulates define what that is for a subatomic system moving slowly the domain of quantum mechanics. So as we take our first step finally into the turf into the domain of the quantum world behold the first postulate of quantum mechanics we represent the state of a quantum system by an arrow in an infinite dimensional space. Now stop something. Don't don't hit next. Don't go to the next episode. Don't don't pause it. It's OK. It's OK. It's OK. Hold my hand. Take three deep breaths. We got this. I believe in you. Don't worry about this. First postulate if it's a little too abstract, swallow I If it's a little bit too much, I want to get the hardest one over with.
First in quantum mechanics, we have to represent the state in a certain way. In classical physics, non quantum physics. We have, uh a lot more freedom to describe the state of a system. It could just be a list of numbers. Here's here's the ball's position. Velocity acceleration. That's it. In quantum mechanics, we need to represent states by an arrow pointing somewhere in an infinite dimensional space. Infinite dimensional spaces are a little bit weird. We're used to thinking a two D, uh, latitude and longitude, or three dimensional latitude, longitude, and then height or altitude or elevation, which is perpendicular to latitude and longitude. So you know your place on the earth, and then you also know your height, and that's perpendicular to the surface of the earth. Now think of 1/4 dimension perpendicular to all three. Now think of 1/5 dimension perpendicular at all four. And now you can't imagine this because our minds literally can't do it because we can only think in three dimensions, uh, but go all the way up to an infinite number of dimensions.
That's, uh, that's weird, and that's messed up, but it's needed to properly describe the state of a quantum mechanical system. I actually need an infinite number of dimensions, and my state is an arrow sitting in that infinite dimensional grid. I told you it was abstract. And I told you, it's not gonna connect to reality right away, and that's OK. By the way, if there are any nerds in the audience, I know there are. If you've ever worked with four a transforms or the four a series, you're actually working in an infinite dimensional space. You just don't realize it. You're actually not far away from this aspect of quantum mechanics. And I told you it was abstract, and I told you it was weird. But here we are. Don't worry, because we're at the second postulate every observable that is associated with the system. These are the things that I can measure about the system, like the positions of the particles or their energy levels. The observables act on those little arrows and transform them. Specifically, they take those little arrows sitting in that infinite dimensional space and move them around.
This is the first break from classical physics that we're going to see in quantum mechanics. What this is telling us what this postulate is telling us is that observations make changes to the system. I'm studying. This is different. If I'm studying the classical situation of a ball flying through the air, and I make some sort of observation like take a picture or look at it. I don't change the ball itself. I can assume that the action of the ball moving through space is independent of the action of me looking at it. Quantum mechanics is not that clean. Quantum mechanics, the second postulate of quantum mechanics, tells me that the act of observation changes the state of the system. The evolution of the state of the system is not independent of me looking at it.
Instead, observables act on the state itself act on my little arrow, sitting in an infinite dimensional space, and if that's hard to think about, it's OK. I can't visualize it, either. I just know this postulate that the act of observation changes my state, and we're gonna see more of that play out. Behold, the third postulate. Supporters of the show can go to patreon dot com slash PM Sutter. If you were wondering how Neils bore and Heisenberg and Schroedinger came up with patreon, well, there's only one way to find out. That's patreon dot com slash PM stutter to keep supporting this show. The actual third postulate is that when I go to measure one of those observable So I have my list of observables. I know if I actually make an observation, it's going to change the state of the system under study. It's going to affect it. It's not gonna remain independent. The act of observation actually changes what I'm doing. And this kind of sort of makes sense. By the way, in that second posture, because when you're dealing with subatomic particles in order to study them, you have to poke them and prod them.
And because you're only dealing with one or a few particles at a time and they're really, really tiny, they're gonna be affected by what you're doing. If I wanna look at a baseball, I have to shine some light off of it. But it's not gonna affect the baseball itself. If I shine some light on an electron, the electron is gonna notice. The act of observation is going to change the evolution of the system. The third postulate is that when I actually go to do that measurement, sometimes the results I get can have any value they want, and sometimes they're more limited. This is the quantum and quantum mechanics. Our third postulate when I go to measure the position of an electron, say I can have any result I want. If if I put a particle inside of a box and look at where that particle is and ask Hey, particle, what position are you in? It can be anywhere. It can be, uh, right in the middle of the box. It can be like an inch away from the left edge, an inch away from the right edge. It can be a half an inch away a quarter of an inch away, you know, somewhere too vaguely.
Two thirds. It can be anywhere. I say that these results then are continuous. This observable is continuous. It can be anywhere. I can have any number I want, but some observables are more limited, like the energy level of an electron inside of a box or inside of an atom. I don't get any result I want. I can't have any answer I want. That is the quantum in quantum mechanics. So, as an example, let's say you got a kid and you can ask this kid a couple questions can you say? Hey, kid, how tall are you? Now? That kid can tell you any number. I'm 4 ft 11 inches. I'm 4 ft 10 inches and three quarters. I'm 4 ft 10 inches and 9/10. I'm 4 ft and 8.9913287 inches. I can get any number I want. So I I say that this observable of height is continuous.
When I ask the kid how tall they are, that kid tells me any number. It doesn't matter. But then, if I ask that kid Hey kid, what grade are you in? What's different? The choices are limited here. The kid could say first grade. The kid could say eighth grade. The kid could say sixth grade, but the kid can't say 6.5 Grade three and a quarter grade. Oh, I'm in grade 4.268 In quantum mechanics, we say now that this observable is discrete, it it's chunky. My choices are limited, and the third postulate of quantum mechanics says sometimes the results you get are continuous, and sometimes the results you get the observables you get are discrete. The more detailed statement of the third postulate says, When one of those happens and and when is it continuous and when is it discrete? There's a rule for telling us when it's gonna happen. But in general, the third postulate says, Sometimes it's just gonna happen again. This is a break from classical physics.
Classical physics never ran into this. Classical physics never ran into a situation where you had to ask a kid what grade they're in, and there was a limited choice of answers. But that's the quantum in quantum mechanics, the chunkiness, the discreteness of quantum mechanics. Behold the fourth postulate the results I can get when I actually observe a subatomic system. The results I get are going to be random. I don't know exactly what I'll measure until I go to measure it before I measure it. I only have my list of options. Then, after I measure it, I get one of those options with a certain random chance associated with it. We have a very specific rule called the bone rule, in honor of its discoverer, Max Bone. That tells us the probabilities of getting one of our possible results. But the fourth postulate tells us that randomness and probabilities play a central role in the theory. Again, this is a break from classical mechanics going back to our kid.
Let's say I don't know the kids height or grade until I ask When I approached this kid and I'm gonna ask them a question, it's not like the kid knows their height and knows their grade. And then I just have to ask and discover it like there's some hidden knowledge there. And then the active observation reveals that hidden knowledge no quantum mechanics tells us something differently. Quantum mechanics tells us that the height of the kid or the grade the kid is in is unknown even to the kid. Nobody knows what the answer is. There is no hidden knowledge hidden fact that I just need to reveal through observation. What happens before I make my observation is a fuzzy cloud of probabilities. So when I go to ask the kids' grade, what I know from quantum mechanics is that maybe there'll be a 10% chance of the second grade 20% chance of the third grade, 40 percent chance of seventh grade, and so on.
Quantum mechanics allows me to calculate those probabilities. Classical mechanics has no probabilities like that. Classical mechanics will say no, The kid is in this grade. And then when you go to observe, you're gonna reveal that grade with 100% certainty. Quantum mechanics. You don't know what you're going to get until you actually make the observation. Classical physics would allow me from the postulates from the first principles from the equations of motion and all that all it will allow me. Classical mechanics would allow me to predict exactly what grade that kid is in. Quantum mechanics says no. You can only predict a range of probabilities, a range of possible answers. You can calculate those probabilities, but you don't know exactly what you're gonna get. This will make more sense once I include the fifth postulate, which is once I make a measurement and get a result for an observable. Then if I repeat my measurement, I will always get the same result again. Measurement makes things stick.
So, for example, I go up to a kid. I don't see a kid standing in front of me. I see a fuzzy, cloudy, probability based kid. I don't know what their height is until I go ask and all my knowledge of physics, all the knowledge of the evolution of this system following this kid around. Since this kid was born, I've been following this kid and keeping track of this kid, this poor kid. And now when I go to encounter this kid and figure out their height, I don't know their height. All my knowledge of physics and following the evolution of this kid hasn't told me what their height is gonna be. Only a list of probabilities of what their height could be. And then when I actually go to make the measurement, it creates a height. The kid gets assigned a height. When I finally make the act of observation, I say, Hey, kid, what's your height? Boom. The kid says 4 ft 11. The act of observation creates an answer.
The kid didn't know it. I didn't know it. Physics didn't know it. No one in the universe knew what height this kid was gonna be until I went to ask. There seems to be something special in quantum mechanics that transforms random, chaotic probabilities into concrete knowledge, which is weird and will occupy, like half this series what is going on with this act of measurement? Why is it so special? You know, it's one thing to swallow. OK, the act of observation changes the thing I'm studying that that OK, that subatomic world, that's that's pretty weird. It's another thing to say. Well, OK, our ability to make predictions is a little bit cloudy. We can't say for sure what a result will be. We can only give a range of what the result might be. OK, but then this fifth postulate elevates the role of measurement to take a central place in quantum mechanics, which is, once you make a measurement, you get an answer.
One, like the kid doesn't know. It's, uh what grade There It's like like me asking, Hey, kid, what grade are you? In the act of asking? The kid assigns a grade to that kid, and the grades are randomly chosen like the the Imagine A kid is sitting there and at the top of the head there's one of those, like prize wheel things that clicks around like and then where it lands, that's gonna be their grade. And then, until I observe them, until I observe the kids just sitting there and the wheels just spinning and spinning and spinning. There is no grade. This kid has no grade attached to them, and it's just spin the it just spinning. And then I go up and say, Hey, kid, what's your grade? What grade are you in? And then that makes the wheel slow down and stop the act of me asking assigns. The probability assigns the result. It go to third grade. The kid says. I'm in the third grade. That kid now exists in the third grade. They walk into the third grade classroom.
I go to a different kid. That wheel is spinning. They have no grade yet. They are not in a classroom yet until I walk up to the kid and I said, Hey, kid, what grade are you in? And then that one slows down to I'm in the seventh grade. They are now exist in the seventh grade. The act of observation changes the state of quantum mechanical systems, and in fact, it assigns them to certain results. Results that do not exist until I make the measurement. Prior to the measurement, the best I can do with my laws of physics. My time, evolution and tracking and doing everything to I is is predict a range of possibilities with various probabilities. That's all I can do in quantum mechanics until I actually make the observation in. In classical physics, this never comes up. If I throw a ball, freeze it in a moment in time, calculate it stayed in all its observables, then I can use Newton's laws to tell you exactly where that ball is gonna go.
My act of observation did not impact the ball. I'm gonna know exactly where the ball is gonna go and I can walk away. I can walk away. I don't need to check. I can just turn around and walk away. I'm gonna tell you exactly where the ball is gonna land because it's just gonna obey Newton's laws. And this is classical physics. Quantum mechanics says if I take that frozen moment in time of the baseball and try to make a prediction of where it's gonna go one, the act of observation is going to change the nature of the baseball itself. And two, instead of knowing exactly where the ball is gonna go, I can only calculate a range of probabilities, I can tell you. Well, it might land here. It might land over here, Might land back there. You know, chance this chance, that chance that OK, and if I walk away, I never know exactly where the ball went. If I walk away with Newtonian physics with classical physics, once I walk away, I know exactly where that ball is going. I can predict its future Down to the millimeter. Quantum mechanics. I only have the range of possibilities. That's the fourth postule and then the fifth postule It is that ball doesn't land until I actually measure it until I actually go back and check.
And then it transforms this cloud of probabilities into a specific result with these kids in their classrooms, their grade level, they don't have a grade level. They don't have a home room yet. They don't have an assignment until I make the observation. Until I observe them, I say, Hey, kid, what's your grade? That is an observable. I change their state by interacting with them, and then I actually assign them to a grade by asking the question. The six postulate if my quantum mechanical system is evolving in time it does so according to the Schrodinger equation, seventh postulate. Oh yeah, there's this thing called spin Subatomic particles have this strange property that at first glance makes them behave as tiny spinning Elec electrically charged balls. But on the other hand, it's nothing like that at all. It's all very confusing, and we have to add it in. We are forced to buy experiment. Later, we found we can derive the existence of spin through our knowledge of relativity. But in pure quantum mechanics, we don't have that.
So we just have to say Spin exists. Let me summarize these postulates with the metaphor of the kid. The kid state is everything about that kid, Everything they are and what they're wearing, Uh, what they're feeling at the moment. What what they have for breakfast. Everything. That's their state. But let's say their observables are their height and their grade. These are the things I can actually measure. You can get a kid's precise height, and you can get it. Their exact grade and their height can be any number. It's continuous. Their grade, however, is discrete. It's quantized, but you don't know what their height is and what their grade is in ahead of time. Instead, you can only calculate probabilities of what their grade might be and what their height might be. Once you make your measurement, you'll find the kid in a certain state, you'll find them with a certain height and assigned to a certain grade. If you take repeated measurements, you'll get the same result over and over again. All the unpredictability has disappeared. Once you make your measurement by making your measurement, you have changed the kid's state.
So if I say Hey, kid, what grade are you? Are you are you in? And then the wheel of chan do do do do do. I'm in the fifth grade. The kid walks in the fifth grade. If I ask that kid again. Hey, kid, what grade are you in? They're just getting. I'm in the fifth grade. You already asked me. The act of measurement changes a kid's state. The act of measurement changes the state of an electron in a hydrogen atom. It's observables, an electron in a hydrogen atom. Its observables might be its position or its energy level. Its position is not quantized. Its energy level is when I go to calculate what the energy level might be, what its position might be. I don't know. Ahead of time. I only have a cloud of probabilities of what its position might be and its energy level might be. When I go to make an observation, I change that electron state and it picks a position, and it picks an energy level from that cloud of probabilities. And I have now fixed its state. That's it. Congratulations. You officially know quantum mechanics. You may not understand it, but then again, who does give yourself a pat on the back?
That's the entirety of quantum mechanics. I can't make it any simpler or more abstract than that. Those seven statements are able to capture all the richness, all the beauty and all the downright weirdness of quantum mechanics. Seriously, the entire subatomic world. I can bottle up in those seven statements and notice how crazy abstract is none of the usual quantum stuff you may have heard on this podcast or elsewhere. It's just mathematical statements that's powerful stuff. You're already getting a taste of just how weird and non intuitive quantum mechanics is. But folks, we are just getting started So how did we get here? How did these abstract, weird, semi random statements connect to reality? Well, that's the story for another time, thanks to Mihail E on email at Sharman on Twitter. Massimiliano S on Facebook. Isaac P on email at At Twitter. Chris F on Facebook. Akansha B on email at SMTR on Twitter Albert R on email Julius M on email.
Martin E on email. John T at Facebook Rice C on email Nick on email Jordie R on Twitter at pizza larger at Twitter email HP Arian and email Scott M on email. Graeme Dion email Martin N on email at Sample SAPIENS on TWITTER. Peter W on email at MARK Group on Twitter Sean on email Susan S on email. Daniel Jan email. Campbell Dion email. TIMOTHY BE on YouTube, Fernando Gian email and James W on email. Of course, you can keep contributing to the show. Patreon dot com slash PM Sutter. I really do appreciate it. And my top Patreon contributors Justin G, Chris L, Barbara Kay Duncan M Coy D Justin Z Nate H, Andrew FN, Scott M, Rob H, Justin Lewis M Paul G John W, Alexis Aaron J Jennifer M, Gilbert M, Joshua BH, John S, Thomas D, Michael R and Simon G send questions all the way here all the time. Ask us spaceman at gmail dot com. The website is Ask the spaceman dot com.
You can find me on all social channels. I'm at Paul Mats Sutter. Thank you, everyone for listening. I'll see you next time for more complete knowledge of time and space pulling up to Mickey D's just for drinks. Oh yeah, that's me. Nothing extra. Just perfection and a straw coming in hot for the coldest cups on the block because there are drinks. Then there are drinks from McDonald's. Get a creamy Oreo fr or mccaf smoothie for less with 20% off any purchase of $10 or more only on the APP.
Limited time only at participating. McDonald's valid one time per day. Visit McDonald's app for details